High Performance Algorithms for the Computation of the Hardy Function - Dissemination & Development
ARCHER2-eCSE11-07
PI: Dr David M Lewis (University of Liverpool)
Co-I(s): Dr Ashley Brereton (University of California, Berkeley)
Technical staff: Dr Mario Antonioletti (EPCC, University of Edinburgh)
Subject Area:
Hardy’s Z-function plays an important role in the theory of the Riemann zeta-function ζ(s) for s∈ℂ (e.g. Ivić 2013*) and its deep connection to the distribution of prime numbers. It represents the amplitude of the zeta-function along the critical line s=1⁄2+It, t∈ℝ and is defined by Z(t)=eIθ(t) ζ(1⁄2+It) for θ(t)∈ℝ (Ivić 2013). For many years, computations of Z(t) utilised the classical Riemann-Siegel formula (Ivić 2013), a method which requires O(t1/2) basic operations. Subsequently Hiary (2011) was able to develop a much more efficient set of computational algorithms, with an operational complexity of O(t1/3{log(t)}κ ). In turn this increased efficiency has enabled calculations of Z(t) for much higher values of t~O(1032 ) than previously feasible.
In recent years, in a series of complex technical papers , the PI of the project discovered the aforementioned theoretical formulation of the Hardy Z-function in terms of generalised Gauss sums . The asymptotic characteristics of the parameters governing these sums immediately raised the prospect of the potential of new algorithms designed to evaluate Z(t) very rapidly, using a novel recursive methodology. These new algorithms would have a much lower operational complexity than the O(t1/3 {log(t)}κ) of the previous state of the art codes. The aim of this eCSE project was to turn this “prospect” into a practical reality by developing new, faster, open access Z(t) codes available for general use by the mathematical research community via a suitable repository.
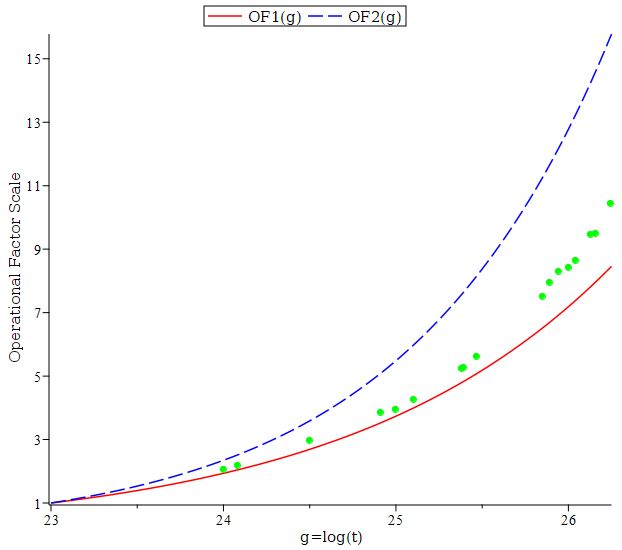
This aim has successfully been realised with the development of the zeta14cubic.f90 code and its variants mentioned above, plus the establishment of the open access repository. The diagram below helps to illustrate the run time reductions achieved by these new codes over and above what was available previously. The horizontal axis shows t≥1023 increasing on a log scale, whilst the vertical axis shows the corresponding increase in run time, measured as a scale factor OFS=(Run time for t >1023)/(Run time for t=1023). The blue and red curves represent the expected increase of OFS with t for algorithms of operational complexity O(t1/3{log(t)}κ) and O(t1/4) respectively. The green dots represent the results of actual runs of the zeta14cubic.f90 code obtained during this eCSE project. All the points lie close to the red curve (the actual complexity is closer to O(t1/4{log(t)}3)) and well below the blue curve, illustrating just how much faster the code developed in this eCSE project is compared to what was previously available to researchers.

The Riemann zeta-function is of fundamental interest in a number of areas of mathematical research, including number theory, theoretical physics, random matrix theory and cryptography. Consequently, these new source codes should be of considerable interest to the mathematical research community and impact on practical applications of these fields to the public sphere.
Information about the code
The application codes are not directly available from ARCHER2. Rather an ARCHER2 account holder would first have to visit the GitHub software repository website at dml2391/Hardy-function-fastcodes: A repository of Fortran/C codes for the rapid calculation of the Hardy function Z(t), using O(t0.25) standard operations in order to download the source codes onto their account. The source codes can then be compiled and run. Instructions about how to do this can be found in the various documentary and sample input files, also to be found in the software repository. In practice, it is all very straightforward.
