uDALES: towards exa-scale simulation of air quality and microclimate in urban environments

ARCHER2-eCSE05-03

---

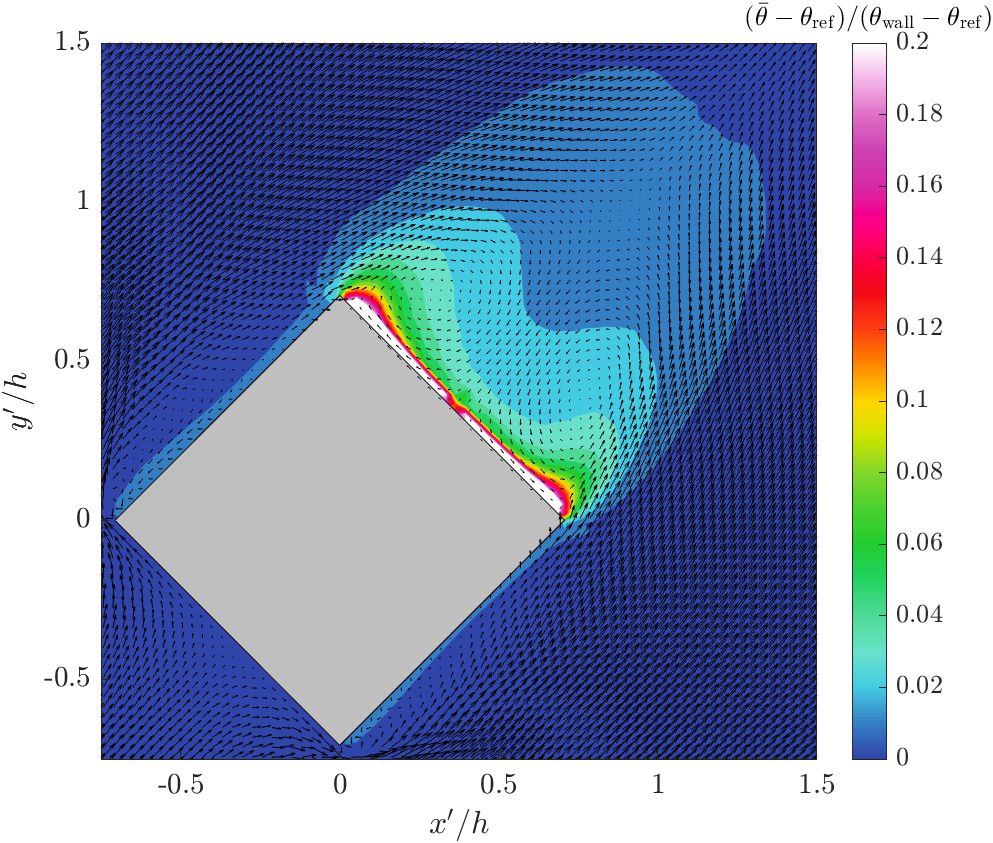
Contours of mean scaled temperature and mean velocity vectors at z/h = 0.5 - rotated

uDALES is a large-eddy simulation (LES) code used to model air quality and microclimate in urban environments.

To improve scalability the 2DECOMP&FFT library was integrated into the uDALES code to enable greater parallelisation than currently possible. As its name suggests, the 2DECOMP&FFT library decomposes computations using a 2-D pencil-based decomposition, exposing more parallelism in a given domain than the 1-D slab-based decomposition currently used by uDALES.

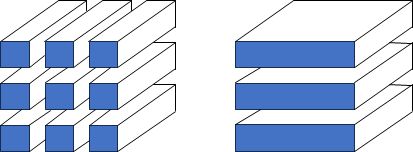
Figure 1: Diagram of pencil-based (left) and slab-based (right) decompositions.

The finite-difference schemes employed by u-DALES require access to neighbouring mesh points, e.g.

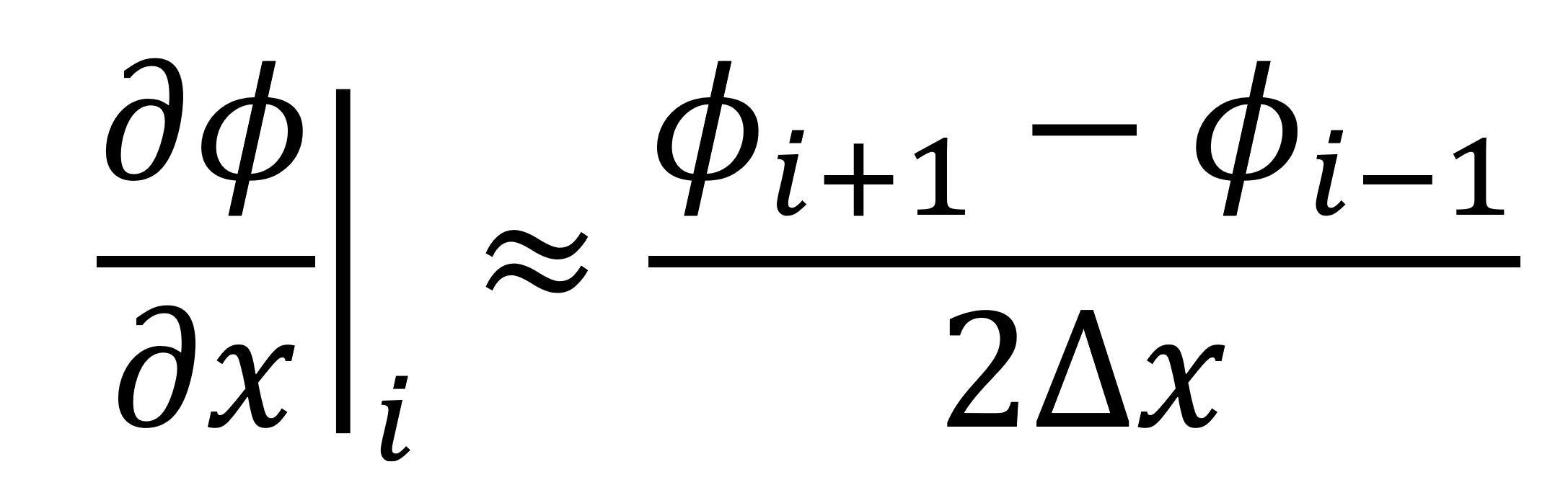
when evaluating derivatives at computational domain boundaries this requires data from the neighbouring domain, stored locally in “halos” that extend the range of each domain. The 2DECOMP&FFT library provides such functionality, including taking care of the extended memory management, however uDALES already allocates its memory with the extended halos defined. To avoid further increasing the memory overhead (one of the goals of this project), the 2DECOMP&FFT halo interface was extended to enable applications to supply their own data buffers with 2DECOMP&FFT handling the parallel data exchange. The existing interface then sits atop this lower-level implementation, allowing this to be contributed upstream.

The Poisson solver in uDALES uses a spectral Poisson solver when the problem is periodic in a given direction. Using the pencil-based decomposition of 2DECOMP&FFT an FFT is performed along the X axis, followed by transposing the transformed data to perform the FFT in the Y axis, followed by transposing into the Z orientation. At this point the approach depends on the Z-boundary conditions, and the grid. In the majority of uDALES cases the Z-direction is non-periodic, and require vertical grid stretching, therefore a finite difference problem is solved in the Z-direction using the Tri-Diagonal Matrix Algorithm. After solution in the Z orientation the process is reversed by transposing back to Y and inverse transforming, followed by the same in X to obtain the pressure solution. This follows the approach taken in Xcompact3D and is known to be scalable.

The scalability of uDALES was assessed on ARCHER2 using two cases of 640x384x384 and 1280x768x768 mesh points, respectively. Figures 1 and 2 show the parallel speedup achieved for each case using up to 128 ARCHER2 nodes (16k cores). For both cases a good scaling is achieved with the smaller maintaining parallel efficiency > 80% up to 4096 cores, corresponding to approximately 23k mesh points per core. A similar limit is observed for a smaller case with the parallel efficiency also dropping beyond about 25k mesh points per core. The larger test case allows scaling to be maintained up to the target of 16,384 CPUs (128 ARCHER2 nodes) as seen by the achieved speedup in Figure 2.

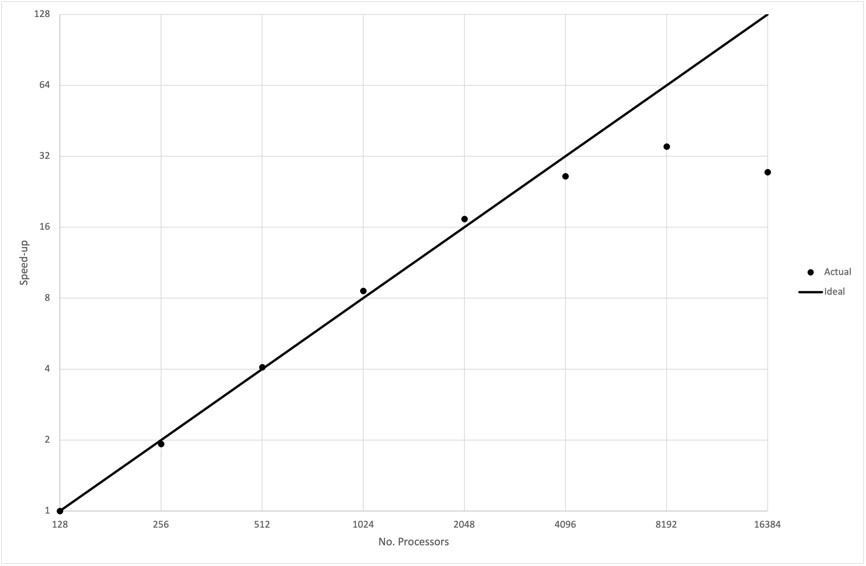
Figure 1 Case 102 scaling

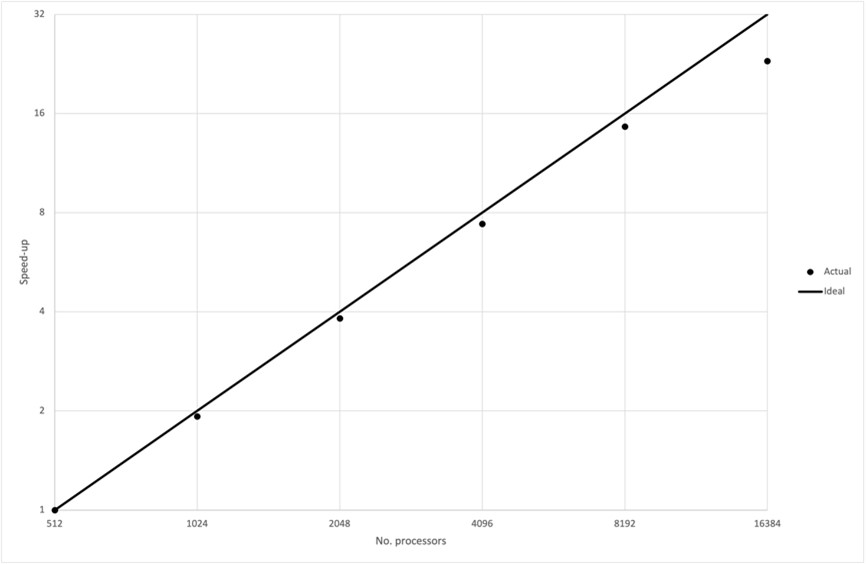
Figure 2 Case 109 scaling

Information about the code

The uDALES code is available via github and can be built on ARCHER2 by loading the PrgEnv-gnu, cray-hdf5-parallel, cray-hdf5netcdf and cmake modules. It includes a forked version of the 2decomp&fft library as a git submodule (the fork is available on github).

Technical Report

Under embargo until August 2024.