Massively parallel and scalable electromagnetic solver for fast analysis of nonlinear optical processes in large clusters of nanoparticles
ARCHER2-eCSE02-12
PI: Prof Nicolae C. Panoiu (University College London)
Technical staff: Dr Ivan Sekulic (University College London)
Subject Area:
Second harmonic generation (SHG) is perhaps the most important nonlinear optical process. It consists of the generation of electromagnetic fields oscillating at twice the frequency of the excitation (linear) fields. As such, a vast number of areas exist where this and similar nonlinear optical processes play a crucial role. Being predominantly a surface effect, with the optical SH sources located at the interface between two optical media, SHG is an indispensable tool for research in surface science, including surface optical microscopy, sensing at the nanoscale and analysis of the shape and morphology of nanoparticles.
When this eCSE project started, OPTIMET was a fast, accurate and scalable solver used for analysis of electromagnetic field scattering in clusters of nanoparticles. At that time, OPTIMET could only handle the scattering of monochromatic waves, namely linear wave scattering whereby the excitation and the scattered fields oscillate at the same frequency. In addition, within the framework of the multiple scattering matrix (MSM) numerical method, OPTIMET allowed the scattering analysis of spherical particles only.
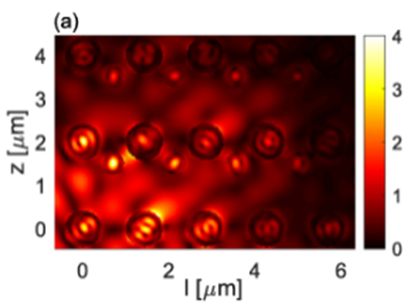
Upon completion of the eCSE-funded project, powerful new functionalities have been added to OPTIMET. A thorough description of this work can be found in a recent article [1]. First, the code was profiled, and several memory bottlenecks were removed, thus improving the linear code. Then, and more importantly, the serial module responsible for the SHG characterisation of a single spherical particle was developed. This initial step is of paramount importance since for this physical setting analytical results exist and thus the SH module can be thoroughly tested and validated. Furthermore, the initial flow of data (the linear fields just below the surface of a particle), representing the output of the linear branch of OPTIMET, which is subsequently input to the nonlinear module, could be tested and the most efficient way of linking the SH module could be determined. Equally important, the serial SH computational module was extended to complex configurations, such as clusters of spherical particles, by introducing the proper translation-addition matrices describing multiple scattering processes within the particle cluster. In the absence of analytical solutions for the case of many spherical particles (in the linear as well as the SH case), we validated our code against a commercially available Finite Element Method (FEM) solver. Even at this stage our code was faster and more accurate than the commercial FEM software and could handle a vastly larger number of particles. All these advantages can be attributed to the nature of the MSM method. An example of field profiles computed with OPTIMET is provided in Figure 1.
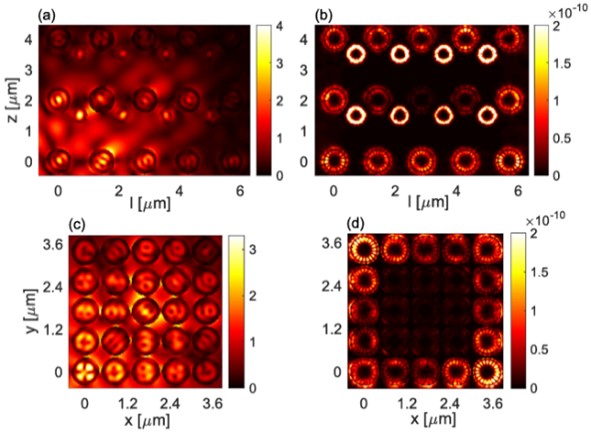
Figure 1. Distribution of the electric field amplitude at Fundamental Frequency (FF) (left panels) and Second Harmonic (SH) (right panels), computed for a non-centrosymmetric (top panels) and centrosymmetric (bottom panels) cluster of silicon nanospheres arranged in a cubic lattice.
In the second part of the project we proceeded with the parallelization of our nonlinear module using the MPI paradigm aimed at execution on distributed memory architectures. All stages of the numerical method at SH were successfully parallelized. The parallelization strategy of the SH scattering matrix assembly follows the linear case for easier code integration. Unlike the linear case, the assembly of the excitation vector at SH was distributed over MPI processes as well because comparatively it is much more computationally demanding. Then we have extended the code to particles of arbitrary shape. For this purpose, we have included a library of meshes of the most common particle morphologies encountered in nanotechnology applications, such as spheres, ellipsoids, cylinders and spheroids. The code was extended accordingly as well, both in the linear and nonlinear cases, to be able to handle such nonspherical particles. Due to the very high computational complexity of such problems, involving demanding integrations over the particle’s surfaces, these routines must be executed in parallel.
Many submatrices stemming from the interaction of distant particles in large clusters are rank deficient because the particles are electromagnetically weakly coupled. In order to exploit this fact, we also developed an efficient matrix compression technique, named adaptive cross approximation (ACA), which was used to compute the low rank approximation of such submatrices in a computationally cheap manner. Serial and parallel versions of ACA alongside Generalized Minimal Residual Method (GMRES) solvers able to operate on compressed matrices were developed and tested. Substantial savings in memory requirements and speedup of the matrix-vector products inherent to GMRES were achieved. As a result of all this software development work, the number of particles that OPTIMET can now handle is at least an order of magnitude larger than what it was before the eCSE-funded project.
[1.] I. Sekulic, J. W. You, and N. C. Panoiu, “T-matrix method for computation of second-harmonic generation upon optical wave scattering from clusters of arbitrary particles”
Information about the code
OPTIMET is successfully installed, developed and tested on ARCHER2 and is available on the path /work/ecseab12/ecseab12/uceeise/OPTIMET/. The executable can be found in the /build/ directory and the source code is in the /src/ directory.
OPTIMET is freely available on GitHub.
